本文来赏析hihoCoder上的一道题目“状态压缩”。我们知道，用动态规划解决问题的时候，状态的表示是很重要的一环。一般来讲，状态可以用一个数组来表示，但是对于有些问题，它们的状态中所包含的信息过多，如果要用数组表示的话，数组的维度会达到四维或以上，这时我们就需要使用状态压缩。状态压缩的核心思想是用二进制位来表示状态，用位运算来表示状态之间的转化。这样不仅减少了空间的消耗，而且提高了程序的效率。

一、题目

背景

小Hi和小Ho决定乘坐火车前往一座城市，但是不幸的是，他们并没有能够买到很好的火车票——他们只能够乘坐最为破旧的火车进行他们的旅程。
火车上的人非常多，以致于都没有足够的位置能让每一个人都有地方坐下来。小Hi和小Ho本着礼让他们的心情——当然还因为本来他们买的就是站票，老老实实的呆在两节车厢的结合处。他们本以为就能够这样安稳抵达目的地，但事与愿违，他们这节车厢的乘务员是一个强迫症，每隔一小会都要清扫一次卫生，而时值深夜，大家都早已入睡，这种行为总是会惊醒一些人。一旦相邻的一些乘客被惊醒了大多数的话，就会同乘务员吵起来，弄得大家都睡不好。
将这一切看在眼里的小Hi与小Ho决定利用他们的算法知识，来帮助这个有着强迫症的乘务员——在不与乘客吵起来的前提下尽可能多的清扫垃圾。
小Hi和小Ho所处的车厢可以被抽象成连成一列的N个位置，按顺序分别编号为1..N，每个位置上都有且仅有一名乘客在休息。同时每个位置上都有一些垃圾需要被清理，其中第i个位置的垃圾数量为Wi。乘务员可以选择其中一些位置进行清理，但是值得注意的是，一旦编号连续的M个位置中有超过Q个的位置都在这一次清理中被选中的话（即这M个位置上的乘客有至少Q+1个被惊醒了），就会发生令人不愉快的口角。而小Hi和小Ho的任务是，计算选择哪些位置进行清理，在不发生口角的情况下，清扫尽可能多的垃圾。

输入与输出

输入数据的第一行为三个正整数N、M和Q，意义如前文所述。
输入数据的第二行为N个整数，分别为W1到WN，代表每一个位置上的垃圾数目。
输出一个整数Ans，表示在不发生口角的情况下，乘务员最多可以清扫的垃圾数目。

二、列出状态转移方程

我们定义F(i,p1,p2,...,p(m-1))表示当前已经完成了第1个位置到第i个位置的清理工作，并且p1表示第i个位置是否被清理（0表示未清理，1表示已清理）、p2表示第i-1个位置是否被清理……p(m-1)表示第i-m+2个位置是否被清理的情况下，最多可以清扫的垃圾数量。注意到，p1...p(m-1)代表从第i个位置往前的连续m-1个位置。
假设我们已经求得了F(i,p1,p2,...,p(m-1))的值，我们来讨论第i+1个位置的清理情况：
如果不清理第i+1个位置，那么我们在该位置的状态可以表示为F(i+1,0,p1,p2,...,p(m-2))，并且由于我们没有在第i+1个位置清理任何垃圾，所以我们清理的垃圾数量相比于第i个位置是没有变化的；
如果要清理第i+1个位置，我们首先要观察是否违反了题目的条件，即p1...p(m-1)中1的数量是否小于Q。如果不小于Q，我们无法清理第i+1个位置；如果小于Q，我们可以清理，此时该位置的状态可以表示为：F(i+1,1,p1,p2,...,p(m-2))，并且由于我们清理了第i+1个位置的垃圾，所以我们清理的垃圾数量相比于第i个位置增加了W(i+1)。
综上所述，我们列出的状态转移方程如下：

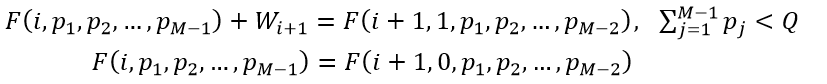
因为每次状态转移都是从i向i+1进行的，所以我们只需要按照i从小到大的顺序进行计算就可以了。最后，我们找到第N个位置上对应的所有状态，这些状态中清理垃圾数量的最大值即为所求。

三、状态压缩

我们如果按照上面的方程求解，那么需要开辟一个维数为M的数组，在M达到两位数的时候显然是不太可能做到的。通过观察发现，对于p1...p(m-1)中的每个p，取值只有0或1两种可能，我们很自然地想到用长度为m-1的二进制串来表示p1...p(m-1)，其最高位代表p1，最低位代表p(m-1)。这样我们动态规划数组的维度可以被直接减少到二维。
此时，我们的方程可以直接写成F(i,j)，其中i的含义和之前相同，j则是上述二进制串对应的十进制整数，其取值范围为0到2^(m-1)-1。
如果不清理第i+1个位置，j的变化相当于右移一位，第一位补0，即：

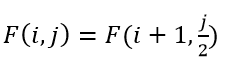
如果要清理第i+1个位置，j的变化相当于右移一位，第一位补1，即：

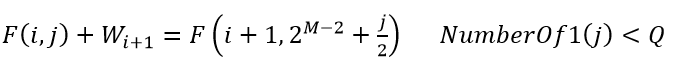
通过状态压缩，我们保存状态只需要开辟N*2^(m-1)大小的空间。在遍历的时候，对于第i行，讨论清理或不清理第i+1个位置的情况，并且填充第i+1行的相应位置。最后观察第N行的所有位置中填充的数据，最大值即为所求。

四、代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

int countFlag(int num){
    int count = 0;
    while(num){
        num &= (num-1);
        count++;
    }
    return count;
}

int main(){
    int N, M, Q;
    cin >> N >> M >> Q;
    vector<int> rubbish(N+1);
    for(int i=1; i<=N; i++)
        cin >> rubbish[i];

    int size = 1 << (M-1);
    vector<vector<int>> table(N+1, vector<int>(size, -1));
    table[0][0] = 0;
    for(int i=0; i<N; i++){
        for(int j=0; j<size; j++){
            if(table[i][j] >= 0){
                //考虑第i+1个位置选还是不选：
                int count = countFlag(j);
                if(count < Q) //可以选择：
                    table[i+1][(1<<(M-2)) + (j>>1)] = max(table[i+1][(1<<(M-2)) + (j>>1)], table[i][j] + rubbish[i+1]);
                //不选的情况：
                table[i+1][j>>1] = max(table[i+1][j>>1], table[i][j]);
            }
        }
    }

    //遍历最后一行，找到最大值：
    int maxRubbish = 0;
    for(int j=0; j<size; j++)
        maxRubbish = max(maxRubbish, table[N][j]);
    cout << maxRubbish;
}